Sort algorithms

Thu, May 7, 2020

1. Introduction

There are many classic sort algirithms, such as follows.

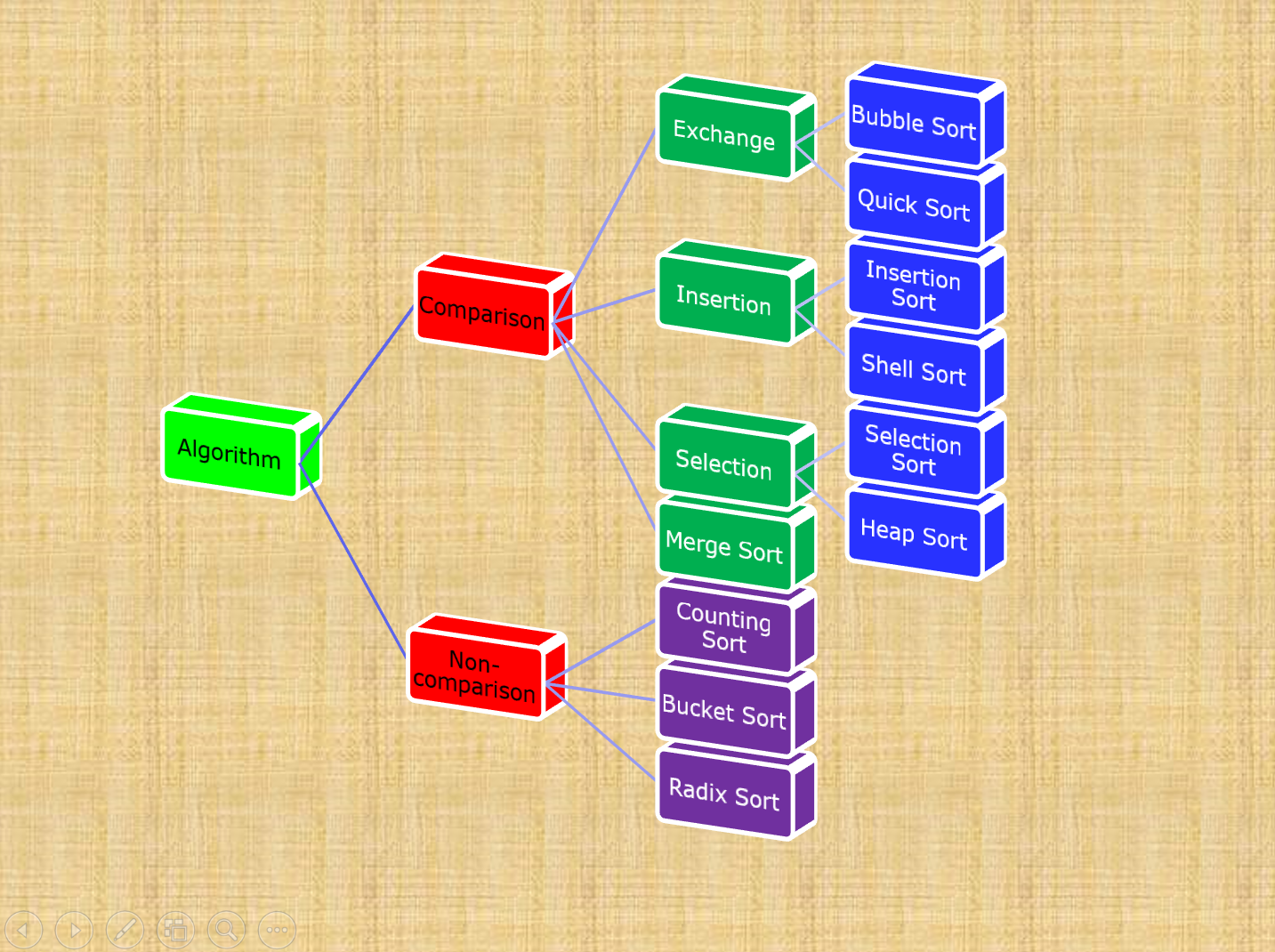
Their algorithm complexity are different, see below. Mathematically, the complexity of comparison sorting algorithm has lower bound O(n log(n)). See details at LINK

2. Bubble sort

It, sometimes referred to as sinking sort, is a simple sorting algorithm that repeatedly steps through the list, compares adjacent elements and swaps them if they are in the wrong order.
Bubble sort has a worst-case and average complexity of O(n^2) where n is the number of items being sorted. Most practical sorting algorithms have substantially better worst-case or average complexity, often O(n log n).
This method requires n-1 rounds and j-1 comparssons at the jth round. Thus, there are n(n-1)/2 comparisons totally.
More details can be found at wiki
There is an animation to illustrate the bubble sort how to be implemented step-by-step, where the original array is

arr[] = {2,6,7,1,9,8,3,4,5};

The animation

The C codes

#include <stdio.h>

#define N 9
void printArrayInt(int *arr, int n, int ncol){
    int i;
    for (i=0; i<n; i++){
        printf("%d   ",arr[i]);
        if(!((i+1)%ncol)) printf("\n");
    }
    printf("\n");
}

void swap(int *arr,int i,int j){
    int temp;
    temp = arr[i];
    arr[i] = arr[j];
    arr[j] = temp;
}

void BubSortInt(int *arr,int n){ 
    int m=n-1,k=0,j,i;
    while(k<m){ 
        j=m; m=0;
        for(i=k; i<j; i++)
            if (arr[i]>arr[i+1]){ 
                swap(arr,i,i+1);
                m=i;
            }
        j=k+1; k=0;
        for(i=m; i>=j; i--)
            if(arr[i-1]>arr[i]){ 
                swap(arr,i,i-1);
                k=i;
            }
    }
}

int main(){
    int arr[]={2,6,7,1,9,8,3,4,5};
    printArrayInt(arr, N, 10);
    BubSortInt(arr,N);
    printArrayInt(arr, N, 10);
    return 0;
}

3. Quick sort

Quicksort is a divide-and-conquer algorithm. It is called “partition-exchange sort” sometimes.
Developed by British computer scientist Tony Hoare in 1959 and published in 1961
When implemented well, it can be about two or three times faster than its main competitors, merge sort and heapsort.
Mathematical analysis of quicksort shows that, on average, the algorithm takes O(n log n) comparisons to sort n items. In the worst case, it makes O(n^2) comparisons, though this behavior is rare.
Algorithm:
- select a ‘pivot’ element from the array and partitioning the other elements into two sub-arrays, according to whether they are less than or greater than the pivot.
- The sub-arrays are then sorted recursively.
More details can be found at wiki
There is an animation to illustrate the quick sort how to be implemented step-by-step, where the original array is

arr[] = {2,6,7,1,9,8,3,4,5};

The animation
The C codes

// Quick sort for an int array
#include<stdio.h>

#include<stdlib.h>

#include<math.h>

#define N 9
void printArrayInt(int *arr, int n, int ncol){
    int i;
    for (i=0; i<n; i++){
        printf("%d   ",arr[i]);
        if(!((i+1)%ncol)) printf("\n");
    }
    printf("\n");
}

void QSortInt(int *arr, int left, int right){
    int i, j,pivot;
    if (left < right){
        i = left; j = right; pivot = arr[i];
        while (i < j){
            while(i < j && arr[j] > pivot) j--;
			if(i < j) arr[i++] = arr[j];
            while(i < j && arr[i] < pivot) i++;
			if(i < j) arr[j--] = arr[i];
        }
        arr[i] = pivot;
        QSortInt(arr, left, i-1);
        QSortInt(arr, i+1, right);
    }
}

int main(){
    int arr[N]={2,6,7,1,9,8,3,4,5};
    printArrayInt(arr, N, 10);
    QSortInt(arr, 0, N-1);
    printArrayInt(arr, N, 10);
    return 0;
}

the corresponding double version can be slightly modified from the above

// Quick sort for an double array
#include<stdio.h>

#include<stdlib.h>

#include<math.h>

#define EPS 1e-6
#define N 100
void printArrayDouble(double *arr, int n, int ncol){
    int i;
    for (i=0; i<n; i++){
        printf("%f   ",arr[i]);
        if(!((i+1)%ncol)) printf("\n");
    }
    printf("\n");
}

void QSortDouble(double *arr, int left, int right){
    int i, j;
    double pivot;
    if (left < right){
        i = left; j = right; pivot = arr[i];
        while (i < j){
            while(i < j && arr[j] > pivot) j--;
			if(i < j) arr[i++] = arr[j];
            while(i < j && arr[i] < pivot) i++;
			if(i < j) arr[j--] = arr[i];
        }
        arr[i] = pivot;
        QSortDouble(arr, left, i-1);
        QSortDouble(arr, i+1, right);
    }
}

int main(){
    int i, index;
    double arr[N], val = 0.16;
    srand(1);
	for(i=0;i<N;i++)
        arr[i] = (rand()%100)/100.0;

    printArrayDouble(arr, N, 10);
    QSortDouble(arr, 0, N-1);
    printArrayDouble(arr, N, 10);
    return 0;
}

4. Selection sort

The algorithm divides the input array into two parts:
- a sorted sublist of items which is built up from left to right at the front (left) of the array
- a subarray of the remaining unsorted items that occupy the rest of the array
Initially, the sorted sublist is empty and the unsorted sublist is the entire input array
The algorithm proceeds by finding the smallest (or largest, depending on sorting order) element in the unsorted subarray, exchanging (swapping) it with the leftmost unsorted element (putting it in sorted order), and moving the sublist boundaries one element to the right.
The time efficiency of selection sort is O(n^2), so there are a number of sorting techniques which have better time complexity than selection sort. One thing which distinguishes selection sort from other sorting algorithms is that it makes the minimum possible number of swaps, n − 1 in the worst case.
More details can be found at wiki
There is an animation to illustrate the Shell sort how to be implemented step-by-step, where the original array is

arr[] = {2,6,7,1,9,8,3,4,5};

The animation

type="video/mp4”
The C codes

// Insertion sort
#include <stdio.h>

#define N 9
void printArrayInt(int *arr, int n, int ncol){
    int i;
    for (i=0; i<n; i++){
        printf("%d   ",arr[i]);
        if(!((i+1)%ncol)) printf("\n");
    }
    printf("\n");
}

void swapInt(int *arr,int i,int j){
    int temp;
    temp = arr[i];
    arr[i] = arr[j];
    arr[j] = temp;
}

void SelectionSort(int *arr, int n){ 
    int i, j, min_idx; 
    for (i = 0; i < n-1; i++){ 
        min_idx = i; 
        for (j = i+1; j < n; j++) 
            if (arr[j] < arr[min_idx]) 
            min_idx = j; 
        swapInt(arr, min_idx, i); 
    } 
}  

int main(){
    int arr[]={2,6,7,1,9,8,3,4,5};
    printArrayInt(arr, N, 10);
    SelectionSort(arr, N);
    printArrayInt(arr, N, 10);

    return 0;
}

5. Heap sort

Heapsort was invented by J. W. J. Williams in 1964.
A binary heap is a heap data structure that takes the form of a binary tree. A binary heap is defined as a binary tree with two additional constraints:
- Shape property: a binary heap is a complete binary tree; that is, all levels of the tree, except possibly the last one (deepest) are fully filled, and, if the last level of the tree is not complete, the nodes of that level are filled from left to right.
- Heap property: the key stored in each node is either greater than or equal to (≥) or less than or equal to (≤) the keys in the node’s children, according to some total order.
There two kep steps
- build a Binary Heap from the given array
- iteration
  - swap the first (the largest key in current array) and the last key
  - rebuild a Binary Heap from the rest array
Although somewhat slower in practice on most machines than a well-implemented quicksort, it has the advantage of a more favorable worst-case O(n log n) runtime. Heapsort is an in-place algorithm, but it is not a stable sort.
More details can be found at wiki
There is an animation to illustrate the quick sort how to be implemented step-by-step, where the original array is

arr[] = {2,6,7,1,9,8,3,4,5};

The animation

The C codes

// Heap sort for an int array
#include<stdio.h>

#include<stdlib.h>

#include<math.h>

#define N 9
void printArrayInt(int *arr, int n, int ncol){
    int i;
    for (i=0; i<n; i++){
        printf("%d   ",arr[i]);
        if(!((i+1)%ncol)) printf("\n");
    }
    printf("\n");
}

void swap(int *arr,int i,int j){
    int temp;
    temp = arr[i];
    arr[i] = arr[j];
    arr[j] = temp;
}

void heapifyInt(int *arr,int i, int n){
    int j=2*i+1, t=arr[i];
    while(j<=n){
        if(j<n && arr[j]<arr[j+1]) j++;
        if(t<arr[j]){
            arr[i]=arr[j];
            i=j;
            j=2*i+1;
        }
        else break;
    }
    arr[i]=t;
	printArrayInt(arr, N, 10);
}

void HeapSortInt(int *arr, int n){
    int i;
    for(i=n/2-1; i>=0; i--)// build heap
        heapifyInt(arr,i,n-1);
    for(i=n-1; i>=1; i--){
        swap(arr,0,i);
        heapifyInt(arr,0,i-1);
    }
}

int main(){
    int arr[N]={2,6,7,1,9,8,3,4,5};
    printArrayInt(arr, N, 10);
    HeapSortInt(arr,N);
    printArrayInt(arr, N, 10);
    return 0;
}

The corresponding double version can be slightly modified from the above

// Heap sort for a double array
#include<stdio.h>

#include<stdlib.h>

#include<math.h>

#define N 100
void printArrayDouble(double *arr, int n, int ncol){
    int i;
    for (i=0; i<n; i++){
        printf("%f   ",arr[i]);
        if(!((i+1)%ncol)) printf("\n");
    }
    printf("\n");
}

void swap(double *arr,int i,int j){
    double temp;
    temp = arr[i];
    arr[i] = arr[j];
    arr[j] = temp;
}

void heapify(double *arr,int i, int n){
    int j=2*i+1;
    double t=arr[i];
    while(j<=n){
        if(j<n && arr[j]<arr[j+1]) j++;
        if(t<arr[j]){
            arr[i]=arr[j];
            i=j;
            j=2*i+1;
        }
        else break;
    }
    arr[i]=t;
}

void HeapSortDouble(double *arr, int n){
    int i;
    for(i=n/2-1; i>=0; i--)// build heap
        heapify(arr,i,n-1);
    for(i=n-1; i>=1; i--){
        swap(arr,0,i);
        heapify(arr,0,i-1);
    }
}

int main(){
    int i;
    double arr[N],*s;
    s=arr;
    srand(1);
	for(i=0;i<N;i++)
        arr[i] = (rand()%100)/100.0;

    printArrayDouble(arr, N, 10);
    HeapSortDouble(s,N);
    printArrayDouble(arr, N, 10);
    return 0;
}

6. Merge sort

Most implementations produce a stable sort, which means that the order of equal elements is the same in the input and output.
Merge sort is a divide and conquer algorithm that was invented by John von Neumann in 1945. A detailed description and analysis of bottom-up mergesort appeared in a report by Goldstine and von Neumann as early as 1948.
Conceptually, a merge sort works as follows:
- Divide the unsorted list into n sublists, each containing one element (a list of one element is considered sorted).
- Repeatedly merge sublists to produce new sorted sublists until there is only one sublist remaining. This will be the sorted list.
More details can be found at wiki.
There is an animation to illustrate the merge sort how to be implemented step-by-step, where the original array is

arr[] = {2,6,7,1,9,8,3,4,5};

The animation
The C codes

// MergeSortInt
#include <stdio.h>

#define N 9
void printArrayInt(int *arr, int n, int ncol){
    int i;
    for (i=0; i<n; i++){
        printf("%d   ",arr[i]);
        if(!((i+1)%ncol)) printf("\n");
    }
    printf("\n");
}

void MergeInt(int *arr,int *temp, int left, int half, int right){
    int i = left, j=half+1, k = left;
    while(i!=half+1 && j!=right+1){
        if(arr[i] > arr[j])
            temp[k++] = arr[j++];
        else
            temp[k++] = arr[i++];
    }
    while(i != half+1)  temp[k++] = arr[i++];
    while(j != right+1)  temp[k++] = arr[j++];
    for(i=left; i<=right; i++)  arr[i] = temp[i];
	//printArrayInt(arr,N,N);
}
 
void MergeSortInt(int *arr, int *temp, int left, int right){
    int half;
    if(left < right){
        half = left + (right-left) / 2;
        MergeSortInt(arr, temp, left, half);
        MergeSortInt(arr, temp, half+1, right);
        MergeInt(arr, temp, left, half, right);
    }
}
 
int main()
{
    int i, temp[N],arr[N]={2,6,7,1,9,8,3,4,5};
	printArrayInt(arr,N,N);
    MergeSortInt(arr, temp, 0, N-1);
	printArrayInt(arr,N,N);
    return 0;
}

the double version from the above.

// MergeSortDouble
#include <stdio.h>

#define N 9
void printArrayInt(double *arr, int n, int ncol){
    int i;
    for (i=0; i<n; i++){
        printf("%f   ",arr[i]);
        if(!((i+1)%ncol)) printf("\n");
    }
    printf("\n");
}

void MergeDouble(double *arr, double *temp, int left, int half, int right){
    int i = left, j=half+1, k = left;
    while(i!=half+1 && j!=right+1){
        if(arr[i] > arr[j])
            temp[k++] = arr[j++];
        else
            temp[k++] = arr[i++];
    }
    while(i != half+1)  temp[k++] = arr[i++];
    while(j != right+1)  temp[k++] = arr[j++];
    for(i=left; i<=right; i++)  arr[i] = temp[i];
	printArrayDouble(arr,N,N);
}
 
void MergeSortDouble(double *arr, double *temp, int left, int right){
    int half;
    if(left < right){
        half = left + (right-left) / 2;
        MergeSortDouble(arr, temp, left, half);
        MergeSortDouble(arr, temp, half+1, right);
        MergeDouble(arr, temp, left, half, right);
    }
}
 
int main()
{
    double temp[N], arr[N]={2,6,7,1,9,8,3,4,5};
    int i;
    printArrayDouble(arr,N,N);
    MergeSortDouble(arr, temp, 0, N-1);
    printArrayDouble(arr,N,N);  
    return 0;
}

7. Insertion sort

Insertion sort is a simple sorting algorithm that builds the final sorted array (or list) one item at a time. It is much less efficient on large lists than more advanced algorithms such as quicksort, heapsort, or merge sort. However, insertion sort provides several advantages:
- Simple implementation: Jon Bentley shows a three-line C version, and a five-line optimized version
- Efficient for (quite) small data sets, much like other quadratic sorting algorithms
- More efficient in practice than most other simple quadratic (i.e., O(n^2) ) algorithms such as selection sort or bubble sort
- Adaptive, i.e., efficient for data sets that are already substantially sorted: the time complexity is O(kn) when each element in the input is no more than k places away from its sorted position
- Stable; i.e., does not change the relative order of elements with equal keys
- In-place; i.e., only requires a constant amount O(1) of additional memory space
- Online; i.e., can sort a list as it receives it
Algorithm
- Insertion sort iterates, consuming one input element each repetition, and growing a sorted output list.
- At each iteration, insertion sort removes one element from the input data, finds the location it belongs within the sorted list, and inserts it there.
- It repeats until no input elements remain.
More details can be found at wiki
There is an animation to illustrate the Shell sort how to be implemented step-by-step, where the original array is

arr[] = {2,6,7,1,9,8,3,4,5};

The animation
The C codes

// Insertion sort
#include <stdio.h>

#define N 9
void printArrayInt(int *arr, int n, int ncol){
    int i;
    for (i=0; i<n; i++){
        printf("%d   ",arr[i]);
        if(!((i+1)%ncol)) printf("\n");
    }
    printf("\n");
}

void InsertionSort(int *arr, int n) 
{ 
    int i, temp, j; 
    for (i = 1; i < n; i++) { 
        temp = arr[i]; 
        j = i - 1; 
        while (j >= 0 && arr[j] > temp) { 
            arr[j + 1] = arr[j]; 
            j = j - 1; 
        } 
        arr[j + 1] = temp; 
    } 
} 

int main(){
    int arr[]={2,6,7,1,9,8,3,4,5};
    printArrayInt(arr, N, 10);
    InsertionSort(arr, N);
    printArrayInt(arr, N, 10);
    return 0;
}

8. Shell Sort

Shellsort, also known as Shell sort or Shell’s method, is an in-place comparison sort. It can be seen as either a generalization of sorting by exchange (bubble sort) or sorting by insertion (insertion sort).
Donald Shell published the first version of this sort in 1959.
Algorithm
- A list is called h-sorted so that starting anywhere, considering every hth element gives a sorted list。
- Beginning with large values of h, this rearrangement allows elements to move long distances in the original list, reducing large amounts of disorder quickly, and leaving less work for smaller h-sort steps to do.
- If the list is then k-sorted for some smaller integer k, then the list remains h-sorted.
- Following this idea for a decreasing sequence of h values ending in 1 is guaranteed to leave a sorted list in the end.
More details can be found at wiki.
There is an animation to illustrate the Shell sort how to be implemented step-by-step, where the original array is

arr[] = {2,6,7,1,9,8,3,4,5};

The animation
The C codes

#include <stdio.h>

#define N 9
void printArrayInt(int *arr, int n, int ncol){
    int i;
    for (i=0; i<n; i++){
        printf("%d   ",arr[i]);
        if(!((i+1)%ncol)) printf("\n");
    }
    printf("\n");
}

void ShellSortInt(int *p,int n){ 
    int lag=n/2,j,i,t;
    while (lag>0){ 
        for(j=lag; j<n; j++){ 
            t=p[j]; 
            i=j-lag;
            while(i>=0 && p[i]>t){ 
                p[i+lag]=p[i]; 
                i -= lag;
            }
            p[i+lag]=t;
            //printf("lag = %d\t",lag);
            //printArrayInt(p, N, 10);
        }
        lag /= 2;
    }
}

int main(){
    int arr[]={2,6,7,1,9,8,3,4,5};
    printArrayInt(arr, N, 10);
    ShellSortInt(arr,N);
    printArrayInt(arr, N, 10);
    return 0;
}

9. Counting sort

It is an integer sorting algorithm.
It operates by counting the number of objects that have each distinct key value, and using arithmetic on those counts to determine the positions of each key value in the output sequence.
Its running time is linear in the number of items and the difference between the maximum and minimum key values, so it is only suitable for direct use in situations where the variation in keys is not significantly greater than the number of items.
However, it is often used as a subroutine in another sorting algorithm, radix sort, that can handle larger keys more efficiently.
Because counting sort uses key values as indexes into an array, it is not a comparison sort, and the Ω(n log n) lower bound for comparison sorting does not apply to it.
More details can be found at wiki
There is an animation to illustrate the counting sort how to be implemented step-by-step, where the original array is

arr[] = {2,6,6,4,9,8,6,4,5};

The animation
The C codes

// Counting sort for an int array
#include<stdio.h>

#include<stdlib.h>

#define N 9
void printArrayInt(int *arr, int n, int ncol){
    int i;
    for (i=0; i<n; i++){
        printf("%d   ",arr[i]);
        if(!((i+1)%ncol)) printf("\n");
    }
    printf("\n");
}

void CountingSort(int *arr, int n){
    int i, range, max=arr[0], min=arr[0]; 
    for(i=1;i<n;i++){
        if(arr[i]>max) max =arr[i];
        if(arr[i]<min) min =arr[i];
    }
    range = max - min + 1;       
    int *count = (int*)malloc(sizeof(int) * range);
    int *output = (int*)malloc(sizeof(int) * n); 
    for(i = 0; i < range; i++) count[i] =0;
    for(i = 0; i < n; i++) output[i] = 0;

    for(i = 0; i < n; i++) count[arr[i]-min]++;  
    for(i = 1; i < range; i++) count[i] += count[i-1];     
    for(i = n-1; i >= 0; i--) {  
        output[ count[arr[i]-min] -1 ] = arr[i]; 
        count[arr[i]-min]--;  
    }       
    for(int i=0; i < n; i++) arr[i] = output[i]; 
    free(count);
    free(output);
} 

int main(){
    int arr[N]={2,6,6,1,9,8,6,4,5};
    printArrayInt(arr, N, 10);
    CountingSort(arr,N);
    printArrayInt(arr, N, 10);
    return 0;
}

10. Bucket Sort (or Bin sort)

The idea:
- distribute the elements of an array into a number of buckets.
- Each bucket is then sorted individually, either using a different sorting algorithm, or by recursively applying the bucket sorting algorithm.
Bucket sort can be implemented with comparisons and therefore can also be considered a comparison sort algorithm.
The computational complexity depends on the algorithm used to sort each bucket, the number of buckets to use, and whether the input is uniformly distributed.
Algorithm:
- Set up an array of initially empty “buckets”.
- Scatter: Go over the original array, putting each object in its bucket.
- Sort each non-empty bucket.
- Gather: Visit the buckets in order and put all elements back into the original array.
More details can be found at wiki.
There is an animation to illustrate the bucket sort how to be implemented step-by-step, where the original array is

arr[] = {12,6,27,21,39,48,33,34,25,28,31,34,18};

The animation
The C codes

// Bucket sort
#include <stdio.h>

#include <stdlib.h>

#define N 13

int MaxArrayInt(int *arr, int n){
    int i,temp=arr[0];
    for(i=1;i<n;i++)
        if(temp<arr[i]) temp = arr[i];
    return temp;
}

void printArrayInt(int *arr, int n, int ncol){
    int i;
    for (i=0; i<n; i++){
        printf("%d   ",arr[i]);
        if(!((i+1)%ncol)) printf("\n");
    }
    printf("\n");
}

void QSortInt(int *s, int l, int r){
    int i, j,x;
    if (l < r){
        i = l; j = r; x = s[i];
        while (i < j){
            while(i < j && s[j] > x) j--;
			if(i < j) s[i++] = s[j];
            while(i < j && s[i] < x) i++;
			if(i < j) s[j--] = s[i];
        }
        s[i] = x;
        QSortInt(s, l, i-1);
        QSortInt(s, i+1, r);
    }
}

typedef struct bucket 
{
    int count;
    int* value;
};

void BucketSort(int *arr, int n, int NB){
    struct bucket *buckets = (struct bucket *)malloc(sizeof(struct bucket) * NB);
    int i, j, k, m;
    for (i = 0; i < NB; i++){
        buckets[i].count = 0;
        buckets[i].value = (int*)malloc(sizeof(int) * n);
    }    
    for (i = 0; i < n; i++){
        m = arr[i]/10;
        buckets[m].value[buckets[m].count++] = arr[i];
    }
    for (k = 0, i = 0; i < NB; i++){
        if(buckets[i].count>1) QSortInt(buckets[i].value, 0, buckets[i].count-1);
        for(j = 0; j < buckets[i].count; j++)
            arr[k + j] = buckets[i].value[j];
        k += buckets[i].count;
        free(buckets[i].value);
    }
}

int main(){
    int arr[]={12,6,27,21,39,48,33,34,25,28,31,35,18};
    int max, NB=1;
    max = MaxArrayInt(arr,N);
    while (max/=10) NB = max+1;    
    printf("NB = %d\n",NB);

    printArrayInt(arr, N, N);
    BucketSort(arr, N, NB);
    printArrayInt(arr, N, N);
    return 0;
}

11. Radix sort

Radix sort is a non-comparative sorting algorithm. It avoids comparison by creating and distributing elements into buckets according to their radix.
Radix sort dates back as far as 1887 to the work of Herman Hollerith on tabulating machines. Radix sorting algorithms came into common use as a way to sort punched cards as early as 1923.
The first memory-efficient computer algorithm was developed in 1954 at MIT by Harold H. Seward. Computerized radix sorts had previously been dismissed as impractical because of the perceived need for variable allocation of buckets of unknown size.
In the modern era, radix sorts are most commonly applied to collections of binary strings and integers.
More details can be found at wiki.
There is an animation to illustrate the radix sort how to be implemented step-by-step, where the original array is

arr[] = {281, 33, 52, 86, 712, 24, 9, 67, 107, 3, 88, 302};

The animation
The C codes

#include<stdio.h>

#include<stdlib.h>

#define N 12
void printArrayInt(int *arr, int n, int ncol){
    int i;
    for (i=0; i<n; i++){
        printf("%d   ",arr[i]);
        if(!((i+1)%ncol)) printf("\n");
    }
    printf("\n");
}

void CountingRadixSort(int *arr, int *output, int *count, int n, int radix){ 
    int i; 
    for(i = 0; i < 10; i++) count[i] = 0;
    for (i = 0; i < n; i++) count[ (arr[i]/radix)%10 ]++; 
    for (i = 1; i < 10; i++) count[i] += count[i - 1]; 
    for (i = n - 1; i >= 0; i--) { 
        output[count[ (arr[i]/radix)%10 ] - 1] = arr[i]; 
        count[ (arr[i]/radix)%10 ]--; 
    } 
    for (i = 0; i < n; i++) arr[i] = output[i]; 
} 

void RadixSort(int *arr, int n){
    int i, max=arr[0], radix, count[10] = {0};
    int *output = (int*)malloc(sizeof(int) * n); 
    for (i=1;i<n;i++) 
        if(arr[i]>max)  max = arr[i];
    for (radix = 1; max/radix > 0; radix *= 10)
        CountingRadixSort(arr, output, count, n, radix);
    free(output);
}


int main(){
    int arr[] = {281, 33, 52, 86, 712, 24, 9, 67, 107, 3, 88, 302};
    printArrayInt(arr, N, N);
    RadixSort(arr, N);
    printArrayInt(arr, N, N);
    return 0;
}

12. Reference

More information can be found at following websites
https://www.geeksforgeeks.org/
https://www.sanfoundry.com/
https://www.cnblogs.com/onepixel/articles/7674659.html

Homepage

go back to
go back to